| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 티스토리
- K6
- 오라클
- 자바 프로젝트
- hyperledger
- c#
- auto configure
- 자바
- 문법 정리
- 알고리즘
- JVM
- 초대장
- oracle
- 리눅스
- jsp
- 운영체제
- resilience4j
- smart cast
- 학점
- 프로젝트
- 유사코드
- MongoDB
- gradle
- 오라클 디비
- 파이썬 소스
- spring
- dynamic query
- SQL
- 백준 알고리즘
- 파이썬
- Today
- Total
모종닷컴
코틀린에서 소수 다루기 본문
최근 들어 소수점을 다루는 일들이 종종 생깁니다. 그리고 이 소수점들을 이용해 연산을 할 때가 많은데 그러다 보니 소수점 관련 문제들을 마주하게 되면서 BigDecimal을 사용하게 되었습니다. 일단 소수점을 이용해 연산할 때 생기는 문제들에 대해서 살펴보도록 하죠.
소수점 + 소수점 = ?
간단하게 테스트 코드를 만들고 이를 실행시켜보도록 하겠습니다.
class DecimalTest {
@Test
fun `소수점 더하기 테스트`() {
val a = 10.1
val b = 9.2
val c = a + b
print(c)
Assert.assertTrue(c == 19.3)
}
}위의 코드를 실행시키기 전 우리는 코드만 봤을 때는 전혀 문제가 없는 것처럼 보입니다. 하지만 실제로 이 코드를 실행해보면 아래와 같은 결과를 보게 되죠.

엥? 의문이 듭니다. 19.3이 아니라 19.2999999999999 이란 값이 c 변수에 저장이 되어있네요. 이는 바로 컴퓨터가 실수를 표현하는 방식과 관련되어 있습니다.
실수 표현 방식

컴퓨터는 실수 표현할 때 "I'm Sorry"라고 합니다.
컴퓨터에서 실수를 표현하는 방식은 크게 두 가지가 있습니다.
- 고정 소수점 방식
- 부동 소수점 방식
고정 소수점 방식
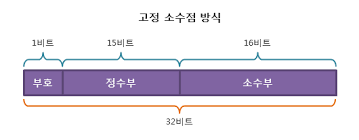
위 사진과 같이 부호, 정수부, 소수부로 나누어져 있습니다. 예를 들어 10.1을 먼저 이진수로 나타내면
1010.0001100110011... 이런 식으로 무한하게 가는데 정수부에는 1010이 들어가고 소수부에는 뒤에 000110011... 16비트가 들어가게 됩니다.
이 방식은 위의 예제처럼 정수부와 소수부 모두 자릿수가 크지 않아 표현할 수 있는 범위가 매우 적다는 단점이 있죠.
부동 소수점 방식
부동 소수점은 고정 소수점 방식과는 다르게 실수를 가수부와 지수부로 나누어 표현합니다. 위에서 추가적인 작업만 하면 되는데 7.625라는 숫자를 먼저 이진수로 나타내 보면 111.101인데 정수부가 1 이 될 때까지 소수점을 옮기고 옮긴 개수(2)만큼을 2² 곱해주면 됩니다. 그러면 7.625 => 1.11101 * 2² 이 되겠죠? 여기서 옮긴 개수 + 127을 더한 값이 지수부이고 소수점 뒤의 숫자 (11101)이 가수부가 됩니다.

앞서 고정 소수점에서 사용했던 10.1은 숫자가 계속 반복되는 형태인데 그렇다 보니 부동 소수점만으로도 표현하기 힘든 숫자가 생기게 되고 테스트 코드 때와 마찬가지로 이상 이상한 값이 들어가게 되는 것이 아닐까 싶습니다.
* 자바의 float은 소수점 6자리까지 표현이 가능하고 double은 15자리까지 표현이 가능하다.
BigDecimal
BigDecimal은 정수와 제곱을 이용하여 숫자를 표기합니다. 위에서 보았듯이 실수는 10진 실수를 2진 실수로 변환할 수 없는 경우가 생겨서 발생한 것이므로 BigDecimal은 이를 정수로 변환하여 다루는 걸로 보여요. BigDecimal에는 precision과 scale이 존재하는데 예를 들어 숫자가 12.345 가 저장되어 있다면 전체 숫자의 길이인 5가 precision 그리고 이중 소수점 밑에 자리 수인 3이 scale이 되는 것이죠.

BigDecimal을 사용할 때 주의할 점이 하나 있는데 아래 사진으로 대체하도록 하겠습니다.

아무튼 BigDecimal 이용해보자.
이제 위의 테스트 코드에서 겪었던 것을 BigDecimal을 이용해 다시 짜 보도록 하겠습니다.
class BigDecimalTest {
@Test
fun `소수점 더하기 테스트 with BigDecimal`() {
val a = BigDecimal("10.1")
val b = BigDecimal("9.2")
val c = a + b
print(c)
Assert.assertTrue(c == BigDecimal("19.3"))
}
}정상적으로 계산이 되었음을 확인할 수 있습니다.
BigDecimal 주의할 점
1. BigDecimal 생성자에 double을 바로 넣는 건 위험

2. BigDecimal 비교할 때는 compareTo를 사용한다. equals 쪽 코드를 타보면 알겠지만 scale이 다르면 틀리다고 해버립니다.
class BigDecimalTest {
@Test
fun `BigDecimal equals 비교`() {
val a = BigDecimal("10.1")
val b = BigDecimal("10.10")
Assert.assertTrue(a == b)
}
@Test
fun `BigDecimal compareTo 비교`() {
val a = BigDecimal("10.1")
val b = BigDecimal("10.10")
Assert.assertTrue(a.compareTo(b) == 0)
}
}3. 나눗셈도 조심해야 한다. RoundingMode를 사용하고 소수점 몇 자리까지 계산할 건지 정하자.
@Test
fun `BigDecimal divide`() {
val a = BigDecimal("1.0")
val b = BigDecimal("3.0")
a.divide(b)
}
@Test
fun `BigDecimal divide with RoundingMode 소수점 3`() {
val a = BigDecimal("1.0")
val b = BigDecimal("3.0")
print(a.divide(b, 3, RoundingMode.HALF_UP))
}
'Programming' 카테고리의 다른 글
| Postman 꿀팁 방출 (0) | 2022.08.07 |
|---|---|
| Github에 파일 크기 및 리포지토리 크기 제한 (0) | 2022.08.05 |
| 테스트 코드는 버그를 찢어 (0) | 2022.07.29 |
| Intellij Code Inspection 사용하기 (0) | 2022.07.24 |
| 우린 서로 다른 버전을 바라보고 있었어..(with 테이블과 엔티티) (0) | 2022.07.20 |




